
One of the functions of a BMS is to balance a battery.
The cells in a battery may be unbalanced in multiple ways, including:
- Actual SOC (State Of Charge)
- Leakage (self discharge current)
- Internal resistance
- Capacity
Only cells from better manufacturers are closely matched, and batteries that use them require very little balancing.
Unfortunately, cells from many manufacturers have significant cell-to-cell variations.
Balancing takes care only of the 1st one: equalizing the SOCs of the various cells in a battery.
In so doing, it compensates also for the 2nd one: cell-to-cell variations in leakage.
Its job may be somewhat hindered by the 3rd one: variations in cell resistance.
What balancing does not do is take care of the 4th one. That's done by a different technique: Redistribution.
Redistribution allows use of all the energy in the battery; it requires significantly higher currents than balancing.
The point of balancing is to maximize the charge that the battery can deliver, limited only by the cell with the lowest capacity.
- Without balancing, the capacity of a battery is limited at one end when a cell becomes fully charged, and at the other end when a cell (same or different cell) becomes fully discharged
- After balancing, the capacity of a battery is limited at both ends by the cell with the lowest capacity (or, in extreme cases, by the cell with the highest internal resistance)
A balanced battery is one in which, at some State Of Charge, all the cells are exactly at the same SOC.
This can be done at any SOC level. In batteries that are regularly charged fully, it is usually done at the 100 % level.
A BMS balances a pack by removing extra charge from the most charged cells, and / or by adding charge to the least charged cells.
Balancing can be dissipative or nondissipative (dissipative: energy is wasted in heat; nondissipative: energy is transferred and therefore it is not wasted).
Dissipative balancing is often called "passive" balancing; nondissipative balancing is often called "active" balancing.
On a first order, how much current is required to balance a battery depends on why the battery is out of balance:
- Gross balancing: to remedy a gross imbalance right after manufacture or repair of a pack that was built using mismatched cells
- Maintenance balancing: keeping the pack in balance during normal use
The proper way to manufacture or repair a pack is to do so in a way that ends up with a balanced pack, so that the BMS is not required to provide an initial, gross balancing.
This can be done in 1 of 2 ways (or both):
- Balance before build: use cells that start at the same State Of Charge (SOC)
- Balance after build: apply a load (or a supply) to the individual cells that are overcharged (or over-discharged), while the pack is still open and there is access to the individual voltage points in the pack
If, on the other side, the pack is built or repaired with no consideration for initial the SOC of individual cells, the BMS may expected to do gross balancing.
In that case, the maximum length of time required to balance that pack will depend on the size of the pack, and the balancing current.
The balancing current required will be proportional to the size of the pack and inversely proportional to the desired balancing time:
Balance current [A] = Pack size [Ah] / gross balancing time [hours]
This graph uses the above formula to show the required balancing time.
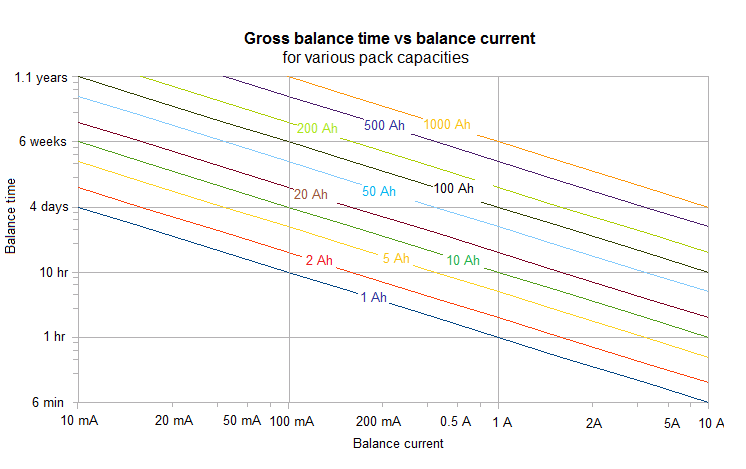
Time required to balance a grossly unbalanced pack, vs. balance current, for various pack sizes.
In the above graph you can see that:
- A BMS with a 1 A balancing current will take almost 1 week to balance a 100 Ah pack that has some cells fully charged, and some cells totally empty
- A balance current of 10 mA will not be able to balance a 1000 Ah pack within the lifetime of its owner
- Conversely, a balance current of 10 A would be an overkill for a 1 Ah pack, as it will balance the pack in less than 6 minutes
Therefore, if the BMS is expected to balance a large, grossly unbalanced pack in a reasonable time, it will have to provide a relatively high balance current.
If a pack starts balanced, keeping in balance is a far easier job: all the BMS has to do is to compensate for the variation in self-discharge leakage in the cells.
- If all the cells have exactly the same leakage, then no balancing is required: the SOC of all the cells will slowly drop exactly the same, so the pack will remain in balance.
- If all the cells have the same leakage, except for one cell whose leakage is 1 mA more, then the BMS has to take, on average, 1 mA from all the other cells to make up for it (or add 1 mA just to the one cell)
So far we looked at the average balancing current (1 mA in the examples above).
In many applications, the BMS is not able to balance 24/7. Yet, leakage discharges a cell 24/7.
In those cases, the balance current has to be higher, in inverse proportion to how much time is available for the BMS to balance.the pack.
For example:
- If the BMS can balance constantly, the balance current can be just 1 mA
- If the BMS is only able to balance for one hour every day, the balance current must be 24 mA to achieve an average of 1 mA
Of course, it is OK if the BMS is able to run more balance current than the required minimum.
In that case, the BMS achieves the required balance current by one of 2 methods:
- Keeping balancing always on, but reducing its value to match the cells' leakage delta current
- Turning balancing on and off with a duty cycle such that, on the average, the current matches the cells' leakage delta current
There is no reason to specify a BMS that can handle more balancing current than is required by the pack in the worst case of leakage current delta.
The balancing current required is proportional to the difference in the leakage current and to what percent of the time is available for balancing:
Balance current [A] = (Max leakage [A] - Min leakage [A]) / (daily balancing time [hours] / 24 [hours])
This graph uses the above formula to show the required balancing current.
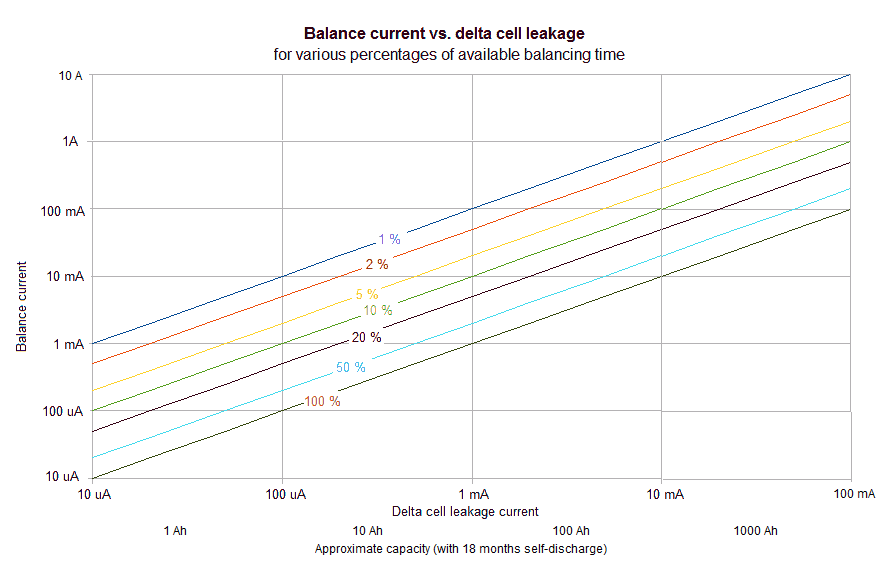
Time required to maintain a pack in balance, vs. delta leakage current, for various proportions of time available for balancing.
Typically, the self-discharge (leakage) current of Li-Ion cells is specified in terms of allowed months in storage at room temperature.
(Actually, very few manufacturers specify it.)
The value is on the order of many months. From that, we can estimate the value of leakage current.
For example, in a 100 Ah pack, if in the worst case the cells are discharged in 18 months, the leakage is:
100 Ah / (18 months * 30 days * 24 hours) = 7.7 mA
Let's assume that some cells have that maximum leakage of 7.7 mA, and all cells have at least 0.7 mA of leakage;
then the delta leakage is 7 mA.
From that, and from how long the BMS can balance, we can see how much balance current is required.
For example, if the BMS is in a vehicle that is plugged for 12 hours every night, charging takes 8 hours, and balancing occurs after charging is completed (4 hours):
Then, the balance current is:
Balance current [A] = 7 mA / (4 hours / 24 hours) = 42 mA
So, in this example, a BMS with a maximum balance current of 100 mA is sufficient to keep the pack in balance.
But what if the delta leakage is 35 mA?
Then, the balance current is:
Balance current [A] = 35 mA / (4 hours / 24 hours) = 210 mA
So, a BMS with a maximum balance current of 100 mA cannot keep this pack in balance.
One way to increase the balance current is to increase the maximum current that the BMS can handle (say, from 100 mA to 1 A).
But another way is to increase the time available for balancing.
In the example above, balancing occurred only after charging was done, leaving only 4 hours for balancing.
But what if the BMS were smart enough to know a priori which cells are likely to need balancing, and do balancing whenever plugged in (12 hours in the example)?
That is the approach taken by the more sophisticated BMSs (e.g.: Texas Instruments).
In that case, in the previous example, the available balancing time would be 12 hours, and the balance current would be:
Balance current [A] = 35 mA / (12 hours / 24 hours) = 70 mA
So, a smart algorithm allowed the same BMS hardware (limited to 100 mA) to handle a pack with five times the leakage.
With a smarter algorithm, a BMS can handle a pack with somewhat more leakage, but only to a point (in practice, a factor of 3 at most).
Beyond that, the hardware itself has to be able to handle more current.
So, how much balance current is required for a Li-Ion pack, during normal operation?
Here are the rules of thumb that Elithion has derived to date:
- 10 mA is sufficient for small back-up supply applications (10 kWh), 100 mA for large applications (100 kWh)
- 100 mA is sufficient to handle any automotive application (10 kWh, plugged in nightly)
- 1 A is sufficient for large pack applications, other than back-up (> 100 kWh, cycled daily)
- Balancing compensates for the SOC of individual cells. It does not compensate for capacity imbalance (which is what Redistribution does).
- A balanced pack is able to supply the maximum charge, limited only by the cell with the least capacity (to supply all the charge, unlimited by any cell, Redistribution is required)
- The single best thing for the sake of a battery pack's balance is that the pack would be built balanced, so that the BMS is not required to do gross balancing
- It makes little economic and engineering sense to specify a BMS that can balance a grossly unbalanced pack just once in its lifetime.
That BMS will be vastly more costly, bulkier and produce far more heat, than a BMS that is designed just for the job that it must do 99 % of the time: keep a previously balanced pack in balance.
Instead, it makes more sense to build packs that are already balanced, so there's no need for a BMS that can perform gross balancing
- If the pack is balanced at the factory, the BMS only needs to be able to handle a balancing current sufficient to compensate for cell-to-cell variations in self-discharge current, during normal operation
- A BMS that provides 100 mA of balancing current is sufficient for most Li-Ion applications
- A smart algorithm that allows balancing all the time can increase a given BMS balancing capability by a factor of about 3
 "How much balancing current do you need?" by Davide Andrea
is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.
Permissions beyond the scope of this license may be available by contacting the author.
"How much balancing current do you need?" by Davide Andrea
is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.
Permissions beyond the scope of this license may be available by contacting the author.
Davide Andrea, Elithion, 2/16/10
 Li-Ion BMS
Li-Ion BMS


