White Paper - Balancing cells by parallelling

Reasoning, methods and time estimates

It is far easier to build a battery pack out of balanced cells, than to balance it after it is built. Balancing by hand is labor intensive and requires a lot of care; and letting the BMS do gross balance can take weeks.

Pre-balancing method

The way to balance cells before building a pack is to connect all of them in parallel, and to let them sit for a while.

Cells in parallel.

Once the cells are connected in parallel, current will flow from the cells with higher SOC to the ones with lower SOC. That's because (in general) the cell voltage increases with SOC level.

The current will start at a high level (as much as 5 C), and decrease exponentially to 0 A as the cells' SOC levels become balanced with respect to each other.

This plot is for 2 cells connected in parallel. The most charged cell (cell 2, blue) disharges into the other cell (cell 1, green). The moment the cells are connected together, their terminal voltage jumps to an average value (orange) and stays there from then on. Their OCVs approach the terminal voltage asymptotically, and their currents approch 0 A asymptotically.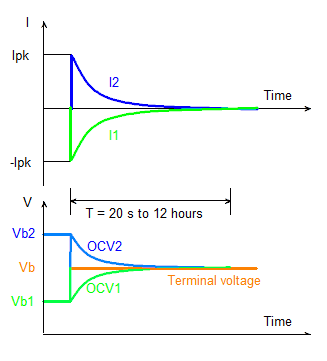

Plot of 2 cells connected in parallel.

CAREFUL! For a few types of cells, if the cells are close to being fully charged, the initial current can be as high as 100 C! That level of current can damage the least charged cells.

Best pre-balancing method

The absolute best way to balance cells is connect cells in parallel that are at 80 % SOC or less, and then use a power supply (3.6 V for Phosphate cells, 4.2 V for LiPo or Cobalt cells) to slowly bring all the cells to 100 % SOC.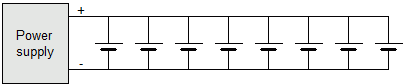

Cells in parallel with a power supply

Of course, this method needs additional time to charge all the cells, from their average SOC to 100 %.

Charging-time [h] = (1 - initial SOC [%] / 100 %) * number of cells * cell capacity [Ah] / supply current [A]

Balancing time

The question is then: how long does it take?

Actually, much faster that you might think: from 20 seconds to 12 hours.

The time depends on:

• Where it is done: at mid SOC levels, or when nearly full
• Internal series resistance of the cell at that SOC
• Slope of the voltage vs. SOC curve at that SOC
• Initial SOC unbalance
• Desired final match of SOC

(Note that the capacity of the cells does not matter.)

The cells' unbalance, the balancing current, and the cells' OCV (Open Circuit Voltage) all decrease with a time constant that is:

Time-constant [h] = Relative resistance of the cell [Ω - Ah] / Voltage drop in the SOC curve [V]

Or, in more practical terms:

Time-constant [m] = 0.6 * Relative resistance [mΩ - Ah] / Slope of voltage vs. SOC curve at that SOC [mV / 1%]

Now that we have the time constant, it is easy to calculate how long it takes to go from a given % SOC unbalance to the desired match of SOC.

Balance-time [m] = Time-constant [m] * e^{(Initial unbalance / Final unbalance)}

One interesting point is that, if all the cells start at mid SOC levels (say, 50 % +/- 30 %), then the moment all the cells are connected together in parallel, the cell voltage will jump to a new value, which corresponds to the average SOC of all the cells. That voltage will remain constant throughout the balancing process. By the time all the cells are balanced, their SOC will all be the same, and equal to the initial average SOC. Therefore, the cell voltage will be exactly the same as the starting voltage. This is regardless of how many cells are used, and regardless of their initial SOC (within the range expressed above). The reason is that, within range of mid SOC levels, the cell resistance and the slope of the voltage vs. SOC are pretty much constant.

On the other side, if some cells start copletely full or completely empty, then their resistance and slope will not be constant. Therefore, the cell voltage will start off at a different voltage, and then, as soon as all the cells enter the mid range, it will quickly settle to the final voltage.

Initial current

The initial relative current is simply:

Initial current [C] = Delta SOC [%] * Slope [mV / 1 %] / Relative resistance [Ω/Ah]

Where "Delta SOC" is difference between the cell's SOC and the average SOC of all the cells.

Or, in terms of actual current:

Initial current [A] = Delta SOC [%] * Slope [mV / 1 %] / Resistance [Ω]

Where "Resistance" is the relative resistance [Ω/Ah] divided by the cell capacitance [Ah].

Examples

For example, the following graph is for a LiFePO4 "power" cells (A123 M1 type) at about 50 % SOC, balanced from 10 % SOC imbalance to 0.1 % match.

Its time constant is about 7.5 minutes and the balance time is about 34 minutes.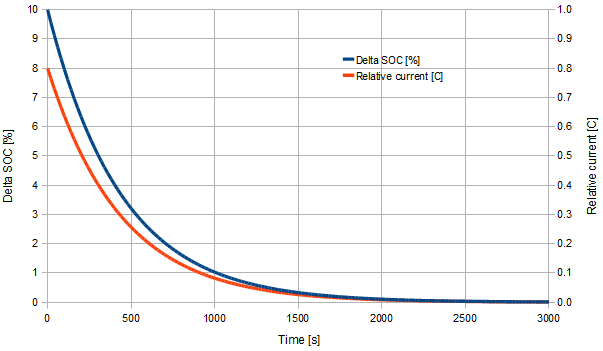

Plot of balancing LiFePO4 "power" cells.

This table lists typical values for variuos types of cells.

The table is divided in 3 sections:

• Mid range: use this section if the cells are at 20 to 80 % SOC
• 100 % SOC, both charging and discharging: use these 2 sections if the cells are nearly full
  • Charging: use this section for the cells that are less charged
  • Discharging: use this section for the cells that are most charged

Each section, lists:

• The cell's relative series resistance at that SOC; to get the actual resistance, divide that value by the capacity; for example, if the relative resistance is 70 mΩ - Ah, and the capacity is 100 Ah, then the actual resistance is 0.7 mΩ
• The slope of the voltage vs. SOC curve for that cell at that SOC: the mV change for each 1 % change in SOC
• The time constant (in minutes) for that cell at that SOC
• The initial relative current (in C) when a cell, whose SOC is off by 10 % from the average, is first connected to other cells; to get the actual current (in Amp), multiply that value by the capacity; for example, if the current is 5 C, and the capacity is 100 Ah, then the current is 500 A
• How long it will take (in minutes) to balance from 10 % to 0.1 % SOC unbalance

The current in red indicates that the initial current exceeds 10 C, which, for many cell types, is excessive. This is particulary a problem for the lowest SOC cells, because the maximum charge current is usually less than the maximum discharge current. Thesefore for those types of cells, never connect cell directly in parallel if they are full.

Type of cell	At mid SOC levels					Charge, close to 100 % SOC					Discharge, close to 100 % SOC
	Rela- tive resis- tance [mΩ - Ah]	Voltage vs. SOC slope [mV / 1%]	Time cons- tant [m]	Initial relative current w/ 10 % unba- lance [C]	Balance time, 10 % to 0.1 % [m]	Rela- tive resis- tance [mΩ - Ah]	Voltage vs. SOC slope [mV / 1%]	Time cons- tant [m]	Initial relative current w/ 10 % unba- lance [C]	Balance time, 10 % to 0.1 % [m]	Rela- tive resis- tance [mΩ - Ah]	Voltage vs. SOC slope [mV / 1%]	Time cons- tant [m]	Initial relative current w/ 10 % unba- lance [C]	Balance time, 10 % to 0.1 % [m]
Power LiFePO4 (A123 M1)	38	2	7.5	0.80	34.5	100	150	0.4	15.0	1.8	25	150	0.1	60.0	0.5
Standard LiFePO4 (CALB)	170	2	51.0	0.12	234.9	680	150	2.7	2.2	12.5	170	150	0.7	8.8	3.1
LiFeYPo4 (Thundersky)	40	0.25	168.0	0.04	773.7	280	100	1.7	3.6	7.7	70	100	0.4	14.3	1.9
LiMn2O2 (GoldPeak)	100	4.5	6.7	0.90	30.7	200	500	0.2	25.0	1.1	50	500	0.1	100.0	0.3
Power LiPo (Kokam SLPB-H5)	15	10	1.2	5.00	5.5	80	30	1.6	3.8	7.4	20	30	0.4	15.0	1.8
Standard LiPo (Kokam SLPB)	120	7.5	9.6	0.63	44.2	480	125	2.3	2.6	10.6	120	125	0.6	10.4	2.7
Cobalt (Sony)	300	6	30.0	0.20	138.2	1200	50	14.4	0.4	66.3	300	50	3.6	1.7	16.6

Formula derivation

The formulae above are derived from an engineering analysis of the electrical circuit consisting of multiple cells in parallel.

First, we want a formula for a cell's time constant at a particular SOC.

From the voltage vs. SOC curve of the cell, we can extract two data points:

• The slope of the voltage over SOC [V/%]; for example, for a LiFePO4 cell at mid SOC levels, it's about 2 mV / 1 % delta SOC.
• The resistance relative to the capacity; we divide the delta between two curves at 50 % SOC, by the delta in the current that caused the curve to shift; for example, for a LiFePO4 "power" cell at mid SOC levels, it's about 25 m&Omega - Ah

Now we'll see how we can use these two data points, together with an analogy with a capacitor, to estimate the time constant of a cell at a partucular SOC.

We have to be careful here: the letter 'C' represents capacity when talking about a capacitor, but it also represents current relative to capacity whent talking about cells.

Had these been capacitors instead of cells, the time constant would be TC [s] = R*C [Ω-Farad], where R is the internal series resistance of the capacitor, and C is its capacitance.

For a cell, instead of resistance we have the resistance relative to capacity; and instead of capacitance we have the slope of the voltage vs. SOC curve.

The voltage over time of a capacitor being discharged has a slope of V/T [V/s] = I/C [A/Farad], where I is the current discharging it, and C is the capacitance.
Or, if we want to solve for capacitance: C [F] = I [A] / (V/T [V/s])

Charge in a cell:

Q [Coulombs] = cell capacity [Ah] * 3600 [s]

Charge in a capacitor:

Q [Coulombs] = Capacity [Farad] * Delta Voltage [V]

Equivalent capacity:

C [Farad] = Charge [Coulombs] / Delta Voltage [V] = Cell capacity [Ah] * 3600 [s] / Delta Voltage [V]

Series resistance:

R [Ω] = Relative resistance [Ω/Ah] / Cell Capacity [Ah]

Time Constant:

TC [s] = R * C =
= Relative resistance [Ω/Ah] / Cell Capacity [Ah] * Cell capacity [Ah] * 3600 [s] /
/ Delta Voltage [V] =
= Relative resistance [Ω/Ah] * 3600 [s] / Voltage [V]

TC [h] = Relative resistance [Ω/Ah] * 3600 [s] / Voltage [V] /
/ 3600 [s] = Relative resistance [Ω/Ah] / Delta Voltage [V]

In more practical units:

TC [m] = Relative resistance [Ω/Ah] / Delta Voltage [V] * 60 =
= Relative resistance [mΩ/Ah] / Delta Voltage [mV] * 0.6 * 100 =
= Relative resistance [mΩ/Ah] / Delta Voltage [mV / 1%] * 0.6